Artigo:

Aplicando a “Metodologia Marchetti” a publicações de Cesare Marchetti

Carlos Feu Alvim

Resumo:

A metodologia de Cesare Marchetti de ajuste de dados históricos, envolvendo uma variada gama de variáveis, por uma curva logística para projetar seu comportamento é descrita aqui tomando como dados os artigos publicados por ele ao longo de sua vida.

O tratamento dos dados é descrito de uma forma didática com objetivo de ajudar a difundir a metodologia. Um cuidado especial é dedicado para a definição do valor máximo a ser alcançado pela variável estudada comumente denominado “nicho”, sendo apresentada uma técnica simples de determinar esta variável crucial dentro da metodologia adotada.

Palavras chave:

Cesare Marchetti, C. Marchetti, logística, ajuste de dados, publicações, análise de sistemas, determinação do nicho

A Metodologia

Buscando prestar uma homenagem a C. Marchetti e difundir sua metodologia, expomos aqui, de uma forma didática, como tratamos a evolução numérica de suas próprias publicações. Ele já havia feito isto com publicações de outros autores e obras de artistas famosos. A lista de publicações do físico italiano, está disponível no portal Cesare Marchetti ^[1].

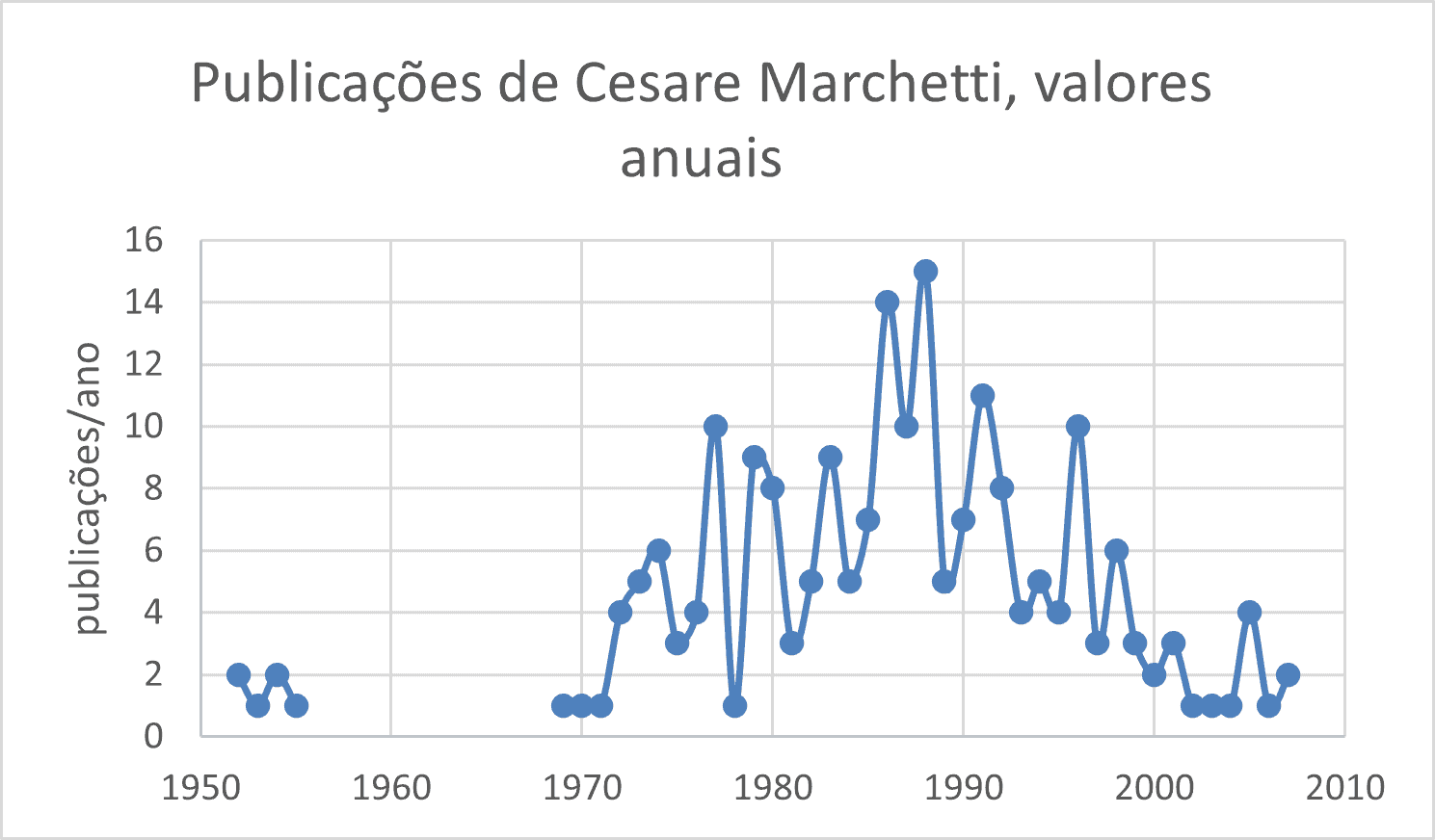
Na Figura 1, está representado o número anual de publicações de C. Marchetti de 1952 a 2007. Ele publicou alguns artigos logo após sua graduação em Pisa (1948), enquanto era pesquisador no Centro Informazioni Studi Esperienze – CISE, em Milão 1950-1955.

Nos anos seguintes, ele esteve trabalhando em laboratórios de empresas industriais ou em áreas como a nuclear onde a divulgação pública de informações é restrita. Certamente era o caso de seus estudos sobre a produção de água pesada, considerada como tecnologia sensível.

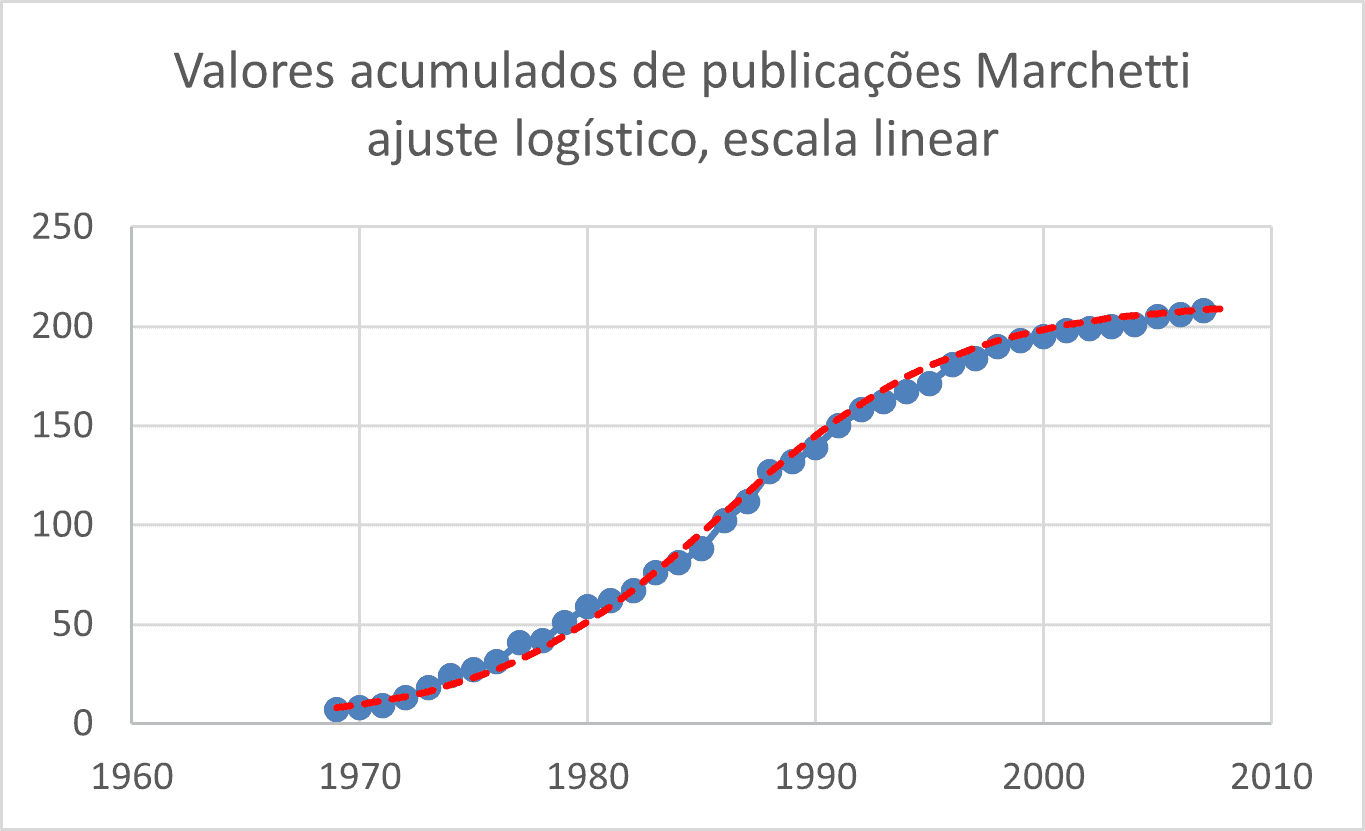
O número de publicações por ano, (Figura 1), está também representado, na forma cumulativa, na Figura 2. O gráfico dessa figura tem  a forma conhecida da curva logística.

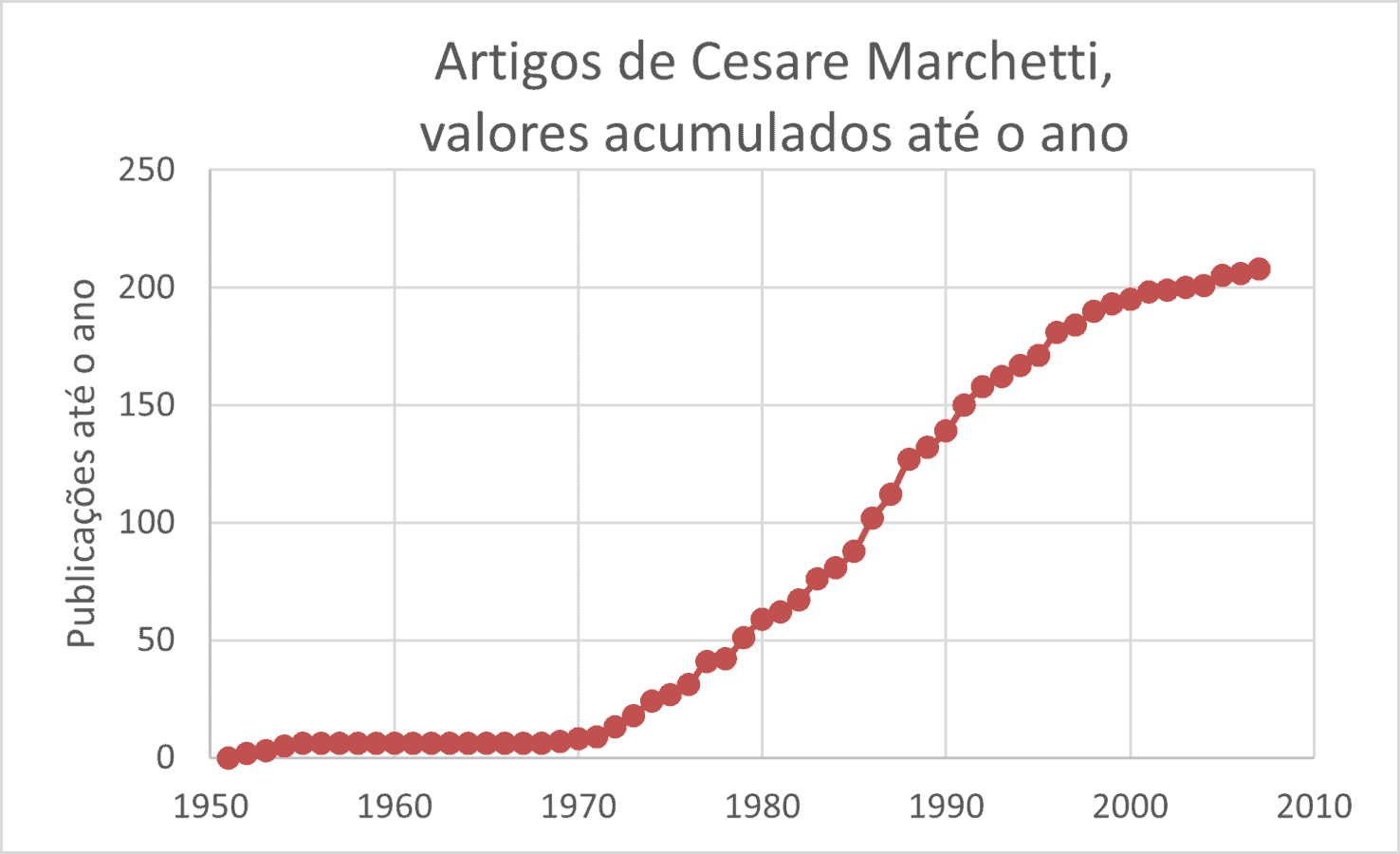
Nossa análise se concentra no período a partir de 1969 que marca o mais importante ciclo de publicação do autor. Foi a partir de sua vinculação ao International Institute for Applied Systems Analysis – IIASA, em Viena, Áustria, em 1974, que sua produção de artigos se tornou mais intensa.

Equações usadas

O tipo de curva logística, mostrado na Figura 1, toma por base a equação diferencial.

dN/dt = c.N.(N*-N)      [1]

No caso, dN representa o acréscimo de publicações no espaço de tempo dt tomado aqui como um ano ( dt =1 ano). No exemplo, c é uma constante, N o número acumulado de publicações e N* é o número total das publicações do autor.

Ou seja, o número de publicações, ao longo do tempo, é proporcional ao número das já publicadas (N) e ao número das publicações que falta publicar (N*-N). Assim, a equação tem um termo crescente e outro decrescente.

Isto significa que um autor que já publicou N artigos tem probabilidade maior de publicar novas obras que um que, na mesma fase da vida, publicou um número menor. Este fator crescente é compensado por um fator decrescente que é o número das que faltam publicar. Isso resulta, na prática, em uma função que cresce nos primeiros anos e decresce nos últimos anos, passando por um máximo que coincide com o ano em que completa a metade do total N*.

Se quisermos usar a metodologia para fazer previsões temos uma aparente incoerência já que um dado futuro (N*) é utilizado nessa previsão. A resposta vem da regularidade das curvas que descrevem a trajetória de publicações tanto para casos similares ao que estamos abordando como para outros fenômenos que apresentam uma dinâmica semelhante. No presente caso, com o autor já falecido, a precisão do método já pode ser testada praticamente para todas, ou quase todas, as publicações.

Em todo o caso, como a última publicação registrada foi de 2007, ainda consideramos como se o número total não estivesse fechado e fazemos projeções para o total que não são muito diferentes entre si e tampouco diferem muito do número registrado na lista usada, de 208 publicações.

A equação que representa uma logística decorre da equação diferencial (1) expressa por

N(t) = N* / [1+ Exp (- (a.t +b))]   [2]

onde a e b são constantes do ajuste.

O ajuste dos dados de publicações ao longo dos anos é feito usando a representação de Fisher-Pry que lineariza a equação

Log [F / (1-F)] = at + b           [3] onde F = N/N*.

Observação: Para facilidade da representação gráfica utilizamos Log10 (logaritmo na base 10) ao invés do LN (logaritmo natural). Isto facilita a correspondência com a escala linear. Naturalmente, na equação [2] deve-se usar, ao invés de exponencial, a potência com base 10.

Ferramentas para a projeção

A principal ferramenta utilizada é a representação dos dados usando a transformada Fisher-Pry para obter as constantes da reta. Esta representação é feita na Figura 3 onde pode-se observar que são mostrados, no eixo vertical, a dupla escala em Log10 (F/(1-F) e o valor de F expresso em percentual.

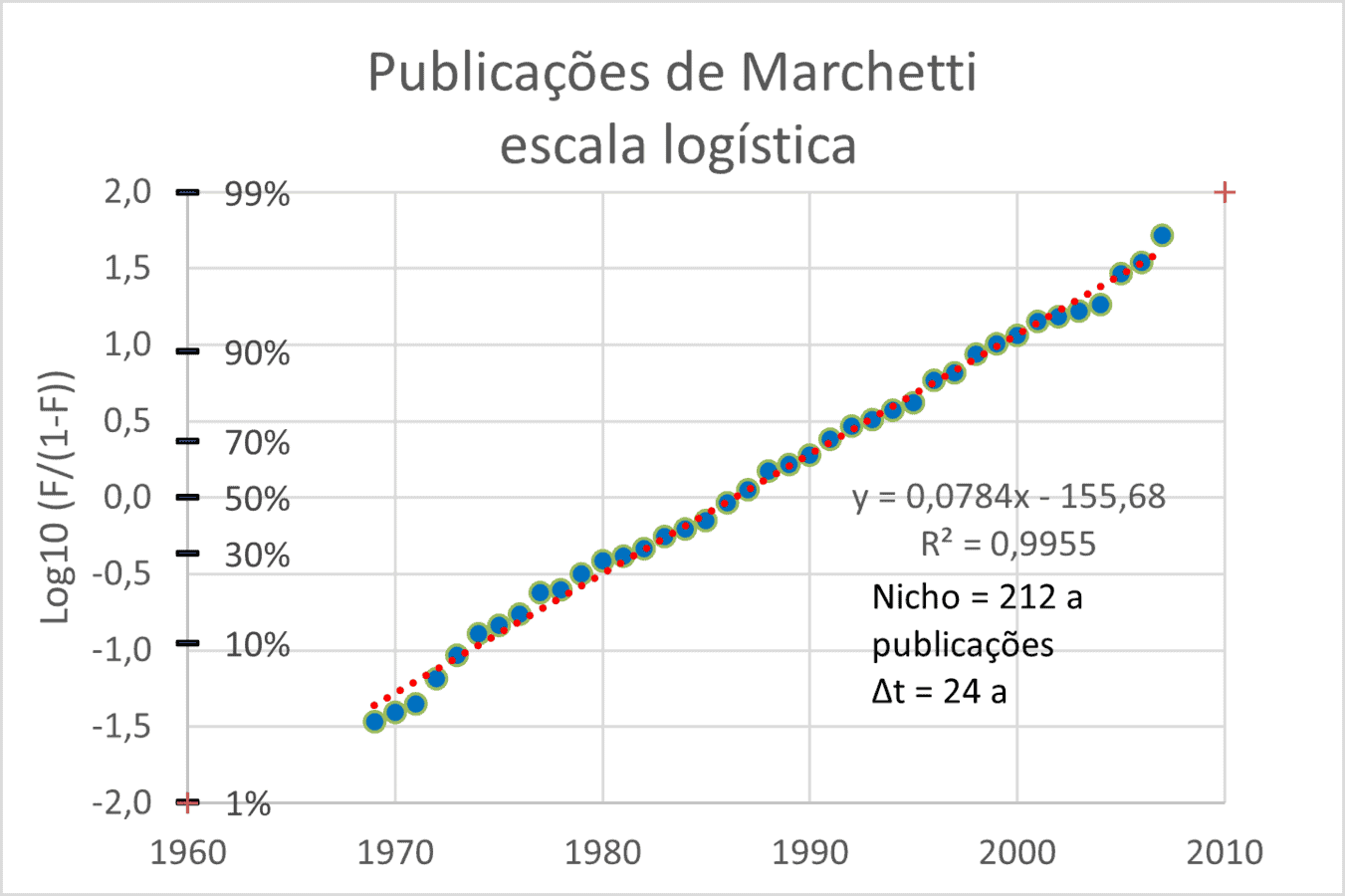
Como pode ser visto na Figura 3 e nos parâmetros relativos ao ajuste, a concordância é muito boa com índice de desvios quadrados R2 = 0,995.

O intervalo de tempo em que o autor levou para passar de 10% de suas publicações para 90% foi de 24 anos, o número total de publicações estimado no ajuste por mínimos quadrados foi de 212, as registradas até o ano de 2007 eram de 208 publicações.

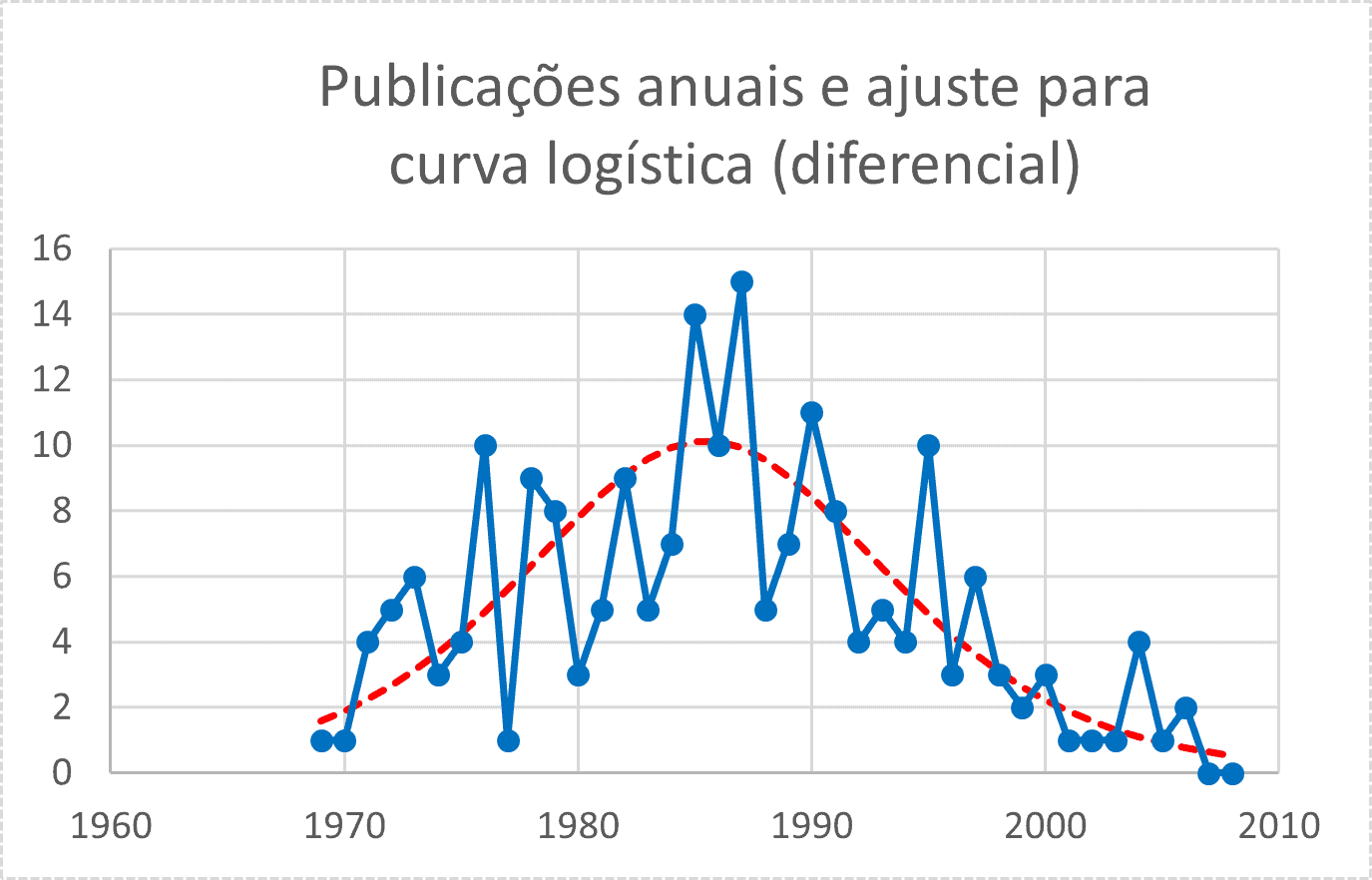
A Figura 4 mostra, em escala linear, a comparação da curva logística em “esse” com o valor acumulado do número de publicações. Também mostramos a curva diferencial, na forma de “sino”, comparada com os valores anuais. Ambas as curvas ajustadas apresentam boa aderência aos dados reais.

As figuras anteriores foram expressas ao longo do tempo (em anos). Na equação diferencial [1] temos o valor das publicações anuais (dN/dt) apenas dependente de N e de duas constantes N* e c.

Podemos apresentar os dados em um gráfico cujo eixo horizontal representa o número N de publicações acumuladas e o eixo vertical representa os valores anuais de publicação (dN/dt). Esta representação fornece informações úteis para a determinação do valor total de publicações ao longo da vida do pesquisador.

A Figura 5 mostra os valores do número de publicações a cada ano. Para eludir as variações anuais muito rápidas os valores de N são representados por uma média móvel 3, centradas para cada ponto[2].

O uso dessa aproximação para determinar N* foi sugerido por Omar Campos Ferreira na E&E n° 46 e aplicado em vários dos artigos publicados nessa revista.

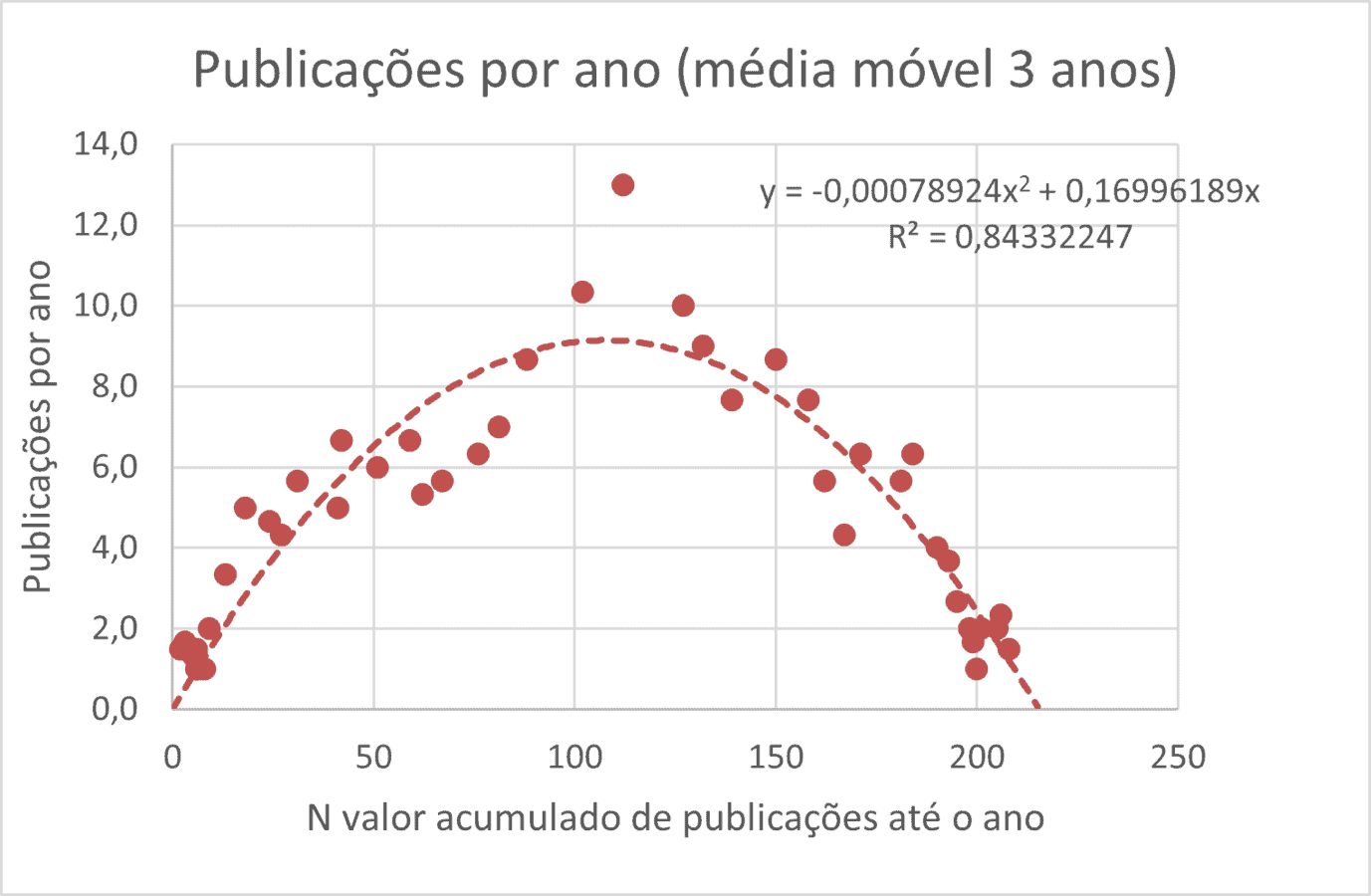
A equação representada é dN/dt = c.N.(N*-N)

que também pode ser expressa como

ΔN =dN/dt = c.N^2 – c.N*.N ou

ΔN = a.N^2 – b.N

onde ΔN é a variação anual onde dt foi tomado como 1 (ano), a e b são as constantes. A fórmula nos permite identificar uma equação de segundo grau que representa uma parábola que passa pelo ponto zero. O ajuste de uma curva de segundo grau nos conduz ao resultado mostrado na Figura 5. Determina-se centro da parábola corresponde N*/2 = 106 que corresponde a N* = 212.

Uma alternativa a esta técnica é representar os dados de ΔN/N, em função de N e obter os parâmetros a e b pelo ajuste de uma reta. O resultado dessa abordagem é mostrado na Figura 6.

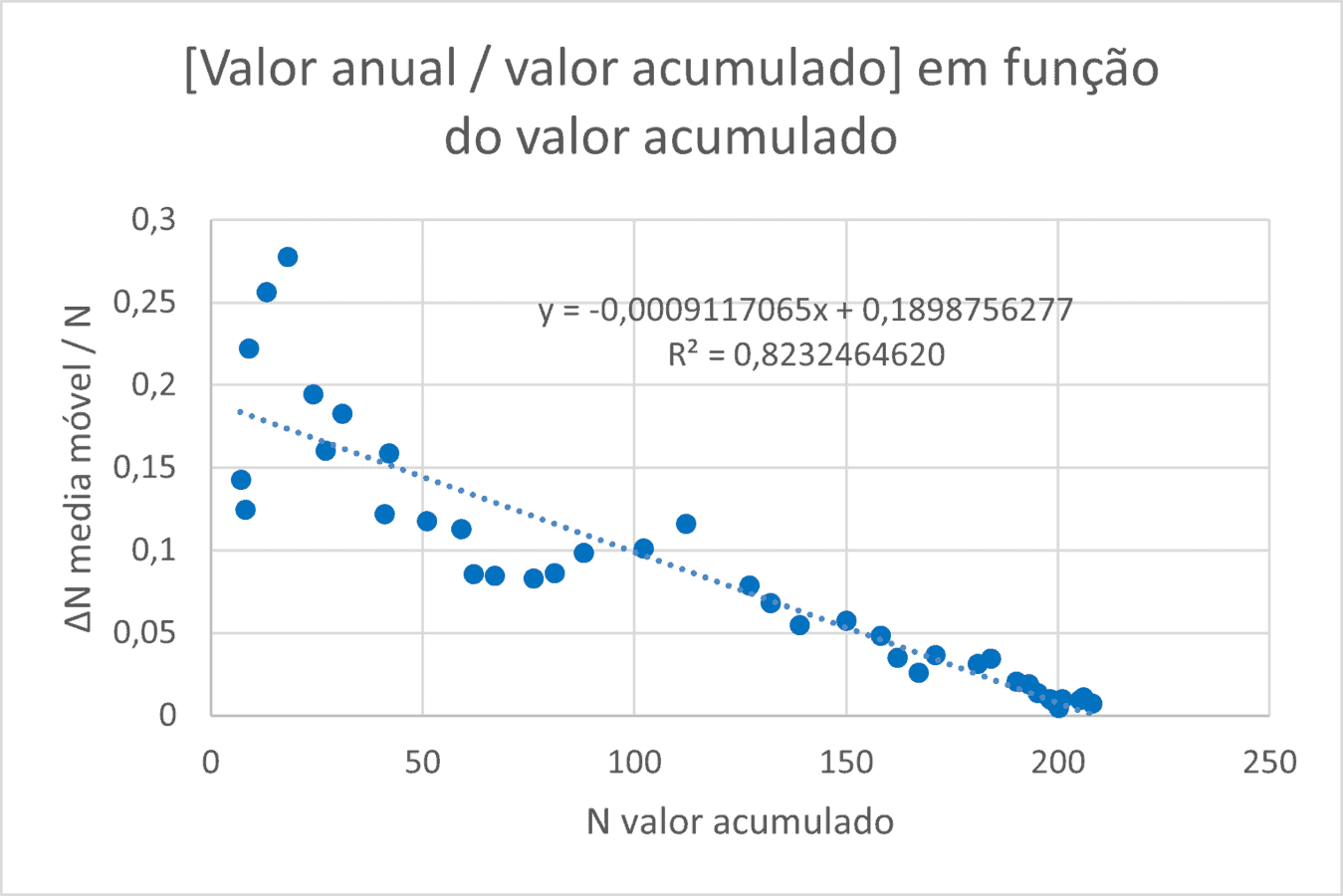
O valor do número de publicações de Cesare Marchetti avaliados por essa metodologia seria de 210 artigos.

Os valores estimados obtidos para o número de publicações total de Cesare Marchetti, recentemente falecido, baseado nos dados disponíveis até 2007 são mostrados na Tabela 1. Observa-se uma boa coincidência nos valores o que é normal por se dispor praticamente do número total ou de um valor muito próximo a ele até aquele ano.

Também mostramos na Tabela 1 o resultado da aplicação das diferentes técnicas aos valores até 1990, quando sabemos que o número de publicações acumuladas atingiu quase 2/3 das publicações totais, os resultados são bastante aceitáveis. As apurações usando as três técnicas para 1990 são mostrados no Anexo. Já os resultados para 1987, que corresponde a cerca da metade do total, estão naturalmente, sujeitos a maiores incertezas e são também mostrados na Tabela 1.

Tabela 1: Valores encontrados para o total de publicações de Cesare Marchetti usando as diversas técnicas

Observação: Em alguns casos, pode-se obter melhores resultados combinando uma das duas últimas técnicas para introduzir o valor inicial de N* no processo iterativo que usa a transformada de Fisher Pry.

Conclusão

A aplicação da Metodologia Marchetti às obras do próprio autor funcionou perfeitamente como mostram as Figuras 3 e 4.

A abordagem de Marchetti tem por finalidade fazer previsões do comportamento de uma variável examinando seu histórico ao longo do tempo.

A aplicação da metodologia a muitos casos, mostra que é necessário chegar ou ultrapassar à metade dos eventos observáveis para que a previsão seja confiável.

Este trabalho propõe uma abordagem, que nos parece inédita, para estimar o parâmetro N* que representa o valor total a ser alcançado em um processo que segue a equação logística. No único conjunto de dados aqui analisados a previsão do total foi melhor que nos outros dois. Além disso, trata-se de uma metodologia mais simples já que envolve apenas o ajuste de uma reta.

Cesare Marchetti que era físico de profissão, nos deixou uma metodologia aplicável a vários sistemas complexos em várias áreas. Sua maior lição é que o futuro é fortemente dependente do passado e que não existem mudanças realmente bruscas em variáveis socioeconômicas e existe um padrão de comportamento que rege a maioria delas.

Anexo: Uso dos dados até 1990 (pouco mais da metade dos pontos) para previsões do total de publicações

Rapidamente, podemos utilizar as ´diferentes técnicas com os dados até o ano de 1990 para testar a capacidade de previsão com o uso das diferentes técnicas apresentadas.

A Figura A1 mostra a aplicação do transformada de Fisher-Pry aos dados até 1990. Os resultados, em termos de previsão, para os anos seguintes foram mostrados na Tabela 1.

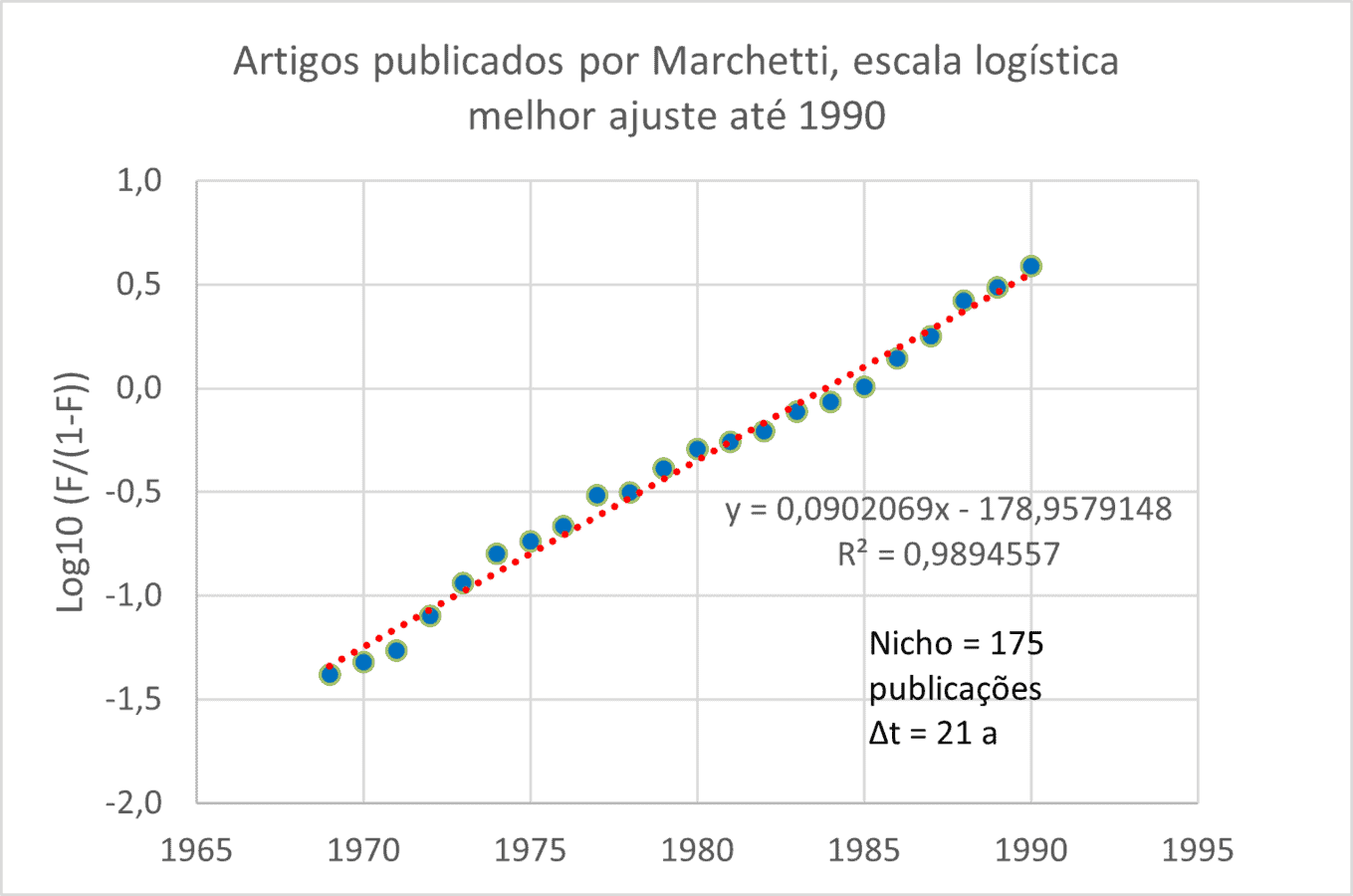
Figura A1: Ajuste de dados 1969 -1990, resultando N* = 142 publicações e tempo para passar de 10% para 90%, 21 anos

A segunda técnica é a utilização da técnica sugerida por Omar Campos Ferreira que consiste em representar os dados anuais em função do número de artigos acumulados até o ano N. A técnica consiste em ajustar uma parábola aos dados disponíveis até 1990, como mostrado na Figura A2.

Os valores ajustados estão mostrados Figura A2 e os dados usados são os da média móvel, assim como foi feito na Figura 5.

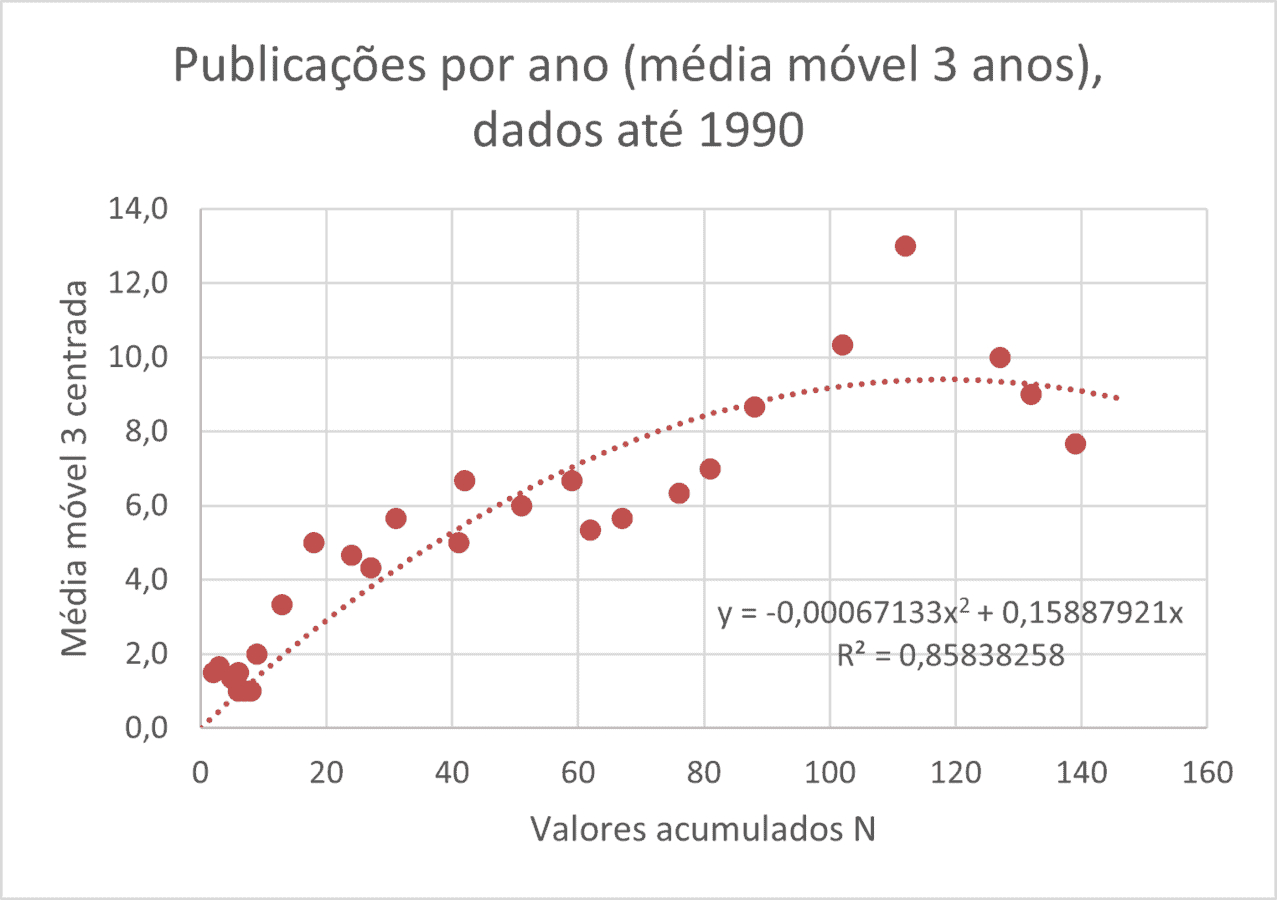
Figura A2: Aplicação da técnica de ajuste de uma parábola que indica N* = 237

O ajuste usando a parábola é muito sensível aos últimos valores da série, o obtido até 1990 (237) está dentro do esperado. Como foi indicado na Tabela 1, o resultado, quando se usa dados até 1987 (432), é muito maior que o obtido com as outras técnicas. Isto pode ser atribuído à grande variação das projeções nos últimos anos quando consideramos o caso “até 1987”.

Enfim, na Figura A3, mostramos os resultados com a técnica de representar o valor de ΔN/N (valor anual / valor acumulado) em função de N e ajustar por eles uma reta.

A intersecção da reta com o eixo horizontal permite estimar o valor de N* ou para y = 0 x = -b/a

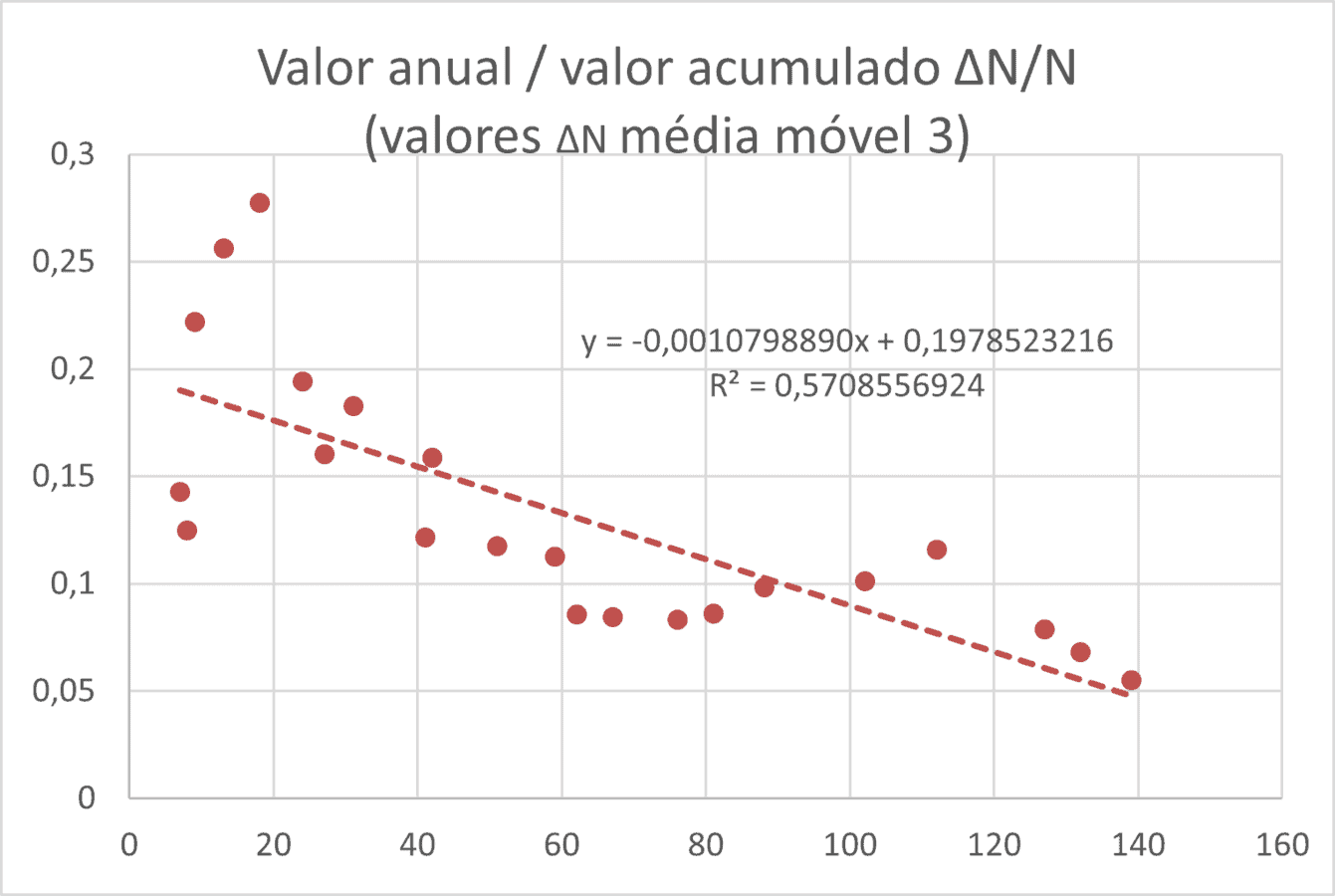
Como pode ser visto na Tabela 1 os valores das diferentes técnicas se aproximam muito, já a de 3 anos antes (1987) apresenta valores bem dispersos. De modo geral, no conjunto de casos que tratamos, observa-se que é necessário ultrapassar o ponto de inflexão dos valores acumulados, metade de N*, para que se tenha uma melhor aproximação da trajetória futura.

_______________________

[1]http://cesaremarchetti.altervista.org/?doing_wp_cron=1687219301.6809539794921875000000  

[2] A média móvel centrada é a média do valor do próprio ponto e os dois valores vizinhos.